Los mapas de radiación solar son una fuente importante de información para los estudios ambientales y ecológicos, de arquitectura o la generación de energía térmica y fotovoltaica. Póngase en contacto con nosotros si necesita mapas de una región diferente o con una resolución espacial o temporal distinta.

Como usar el mapa

Para cambiar de capa entre la radiación solar potencial (cielos despejados con atmósfera) y la radiación solar promedio real con las condiciones climáticas locales, haga clic en el símbolo de la capa en la esquina superior derecha del mapa.

Para mostrar la leyenda haga clic en el signo de información en la esquina inferior derecha.

Cambie zoom y opacidad haciendo clic en los signos o deslizando el control de transparencia que se encuentra en la esquina superior izquierda.

El mapa alcanza el nivel de zoom 12, que es cuando la barra de escala esta a 1 milla o 3 km, y 1 pixel corresponde a 100 m, se puede aumentar el zoom más alta resolución, la capa de imagen satélite se mantiene, pero la capa de radiación solar no es visible.

Se puede usar el mapa en modo pantalla completa haciendo click en el símbolo correspondiente en la esquina superior izquierda, debajo del zoom.

Para buscar una localidad pulse la lupa de búsqueda, pulsándola otra vez se esconde el recuadro de búsqueda.

Mapa de Radiación Solar

Mapa de la media anual de radiación solar diaria sobre la superficie en la provincia de Granada, España, a 100 m de resolución.

Al hacer clic en un punto del mapa aparece una ventana con cuatro valores gráficos de radiación solar:
   Insolación global sobre la superficie del terreno (GSI),
   Insolación global sobre una supeficie horizontal (GHI),
   Insolación directa normal (DNI),
   Insolación difusa,
Los valores globales incluyen la componente difusa modificada por el factor de visión del cielo.

Cómo se realizan estos mapas

Para la radiación solar potencial el cálculo tiene en cuenta el sombreado, la obstrucción del horizonte, temperatura media, humedad y claridad del cielo pero se considera que todos los días son despejados y sin nubes. Por tanto, esta sería la máxima radiación solar media disponible en cada localidad.

Calculamos la posición del sol cada hora desde el amanecer hasta la puesta de sol como un vector 3D, el vector normal a cada celda de la cuadrícula del modelo digital del elevación (DEM), el angulo de incidencia sobre la pendiente y las sombras siguiendo a Corripio (2003). El día juliano, el vector sol-tierra se calculan siguiendo Bourgues (1985), Danby (1988), Meeus (1999) y Rada y Andreas (2003). Para la atenuación de la radiación solar a través de la atmósfera (transmitancia) se utiliza un modelo paramétrico por Bird y Hulstrom (1981a, b) con valores actualizados la constante solar (Kopp y Lean 2011). Hemos comprobado el rendimiento de este modelo con el modelo de transferencia radiativa MODTRAN 4 y da excelentes resultados, así como en otros estudios de intercomparación (Niemelä et al. 2001). La radiación directa se modifica por el ángulo de incidencia en la superficie. Para la radiación difusa se ​tiene en cuenta el factor de visión del cielo y el albedo del terreno circundante.

A continuación hay algunos ejemplos gráficos de la simulación del terreno:

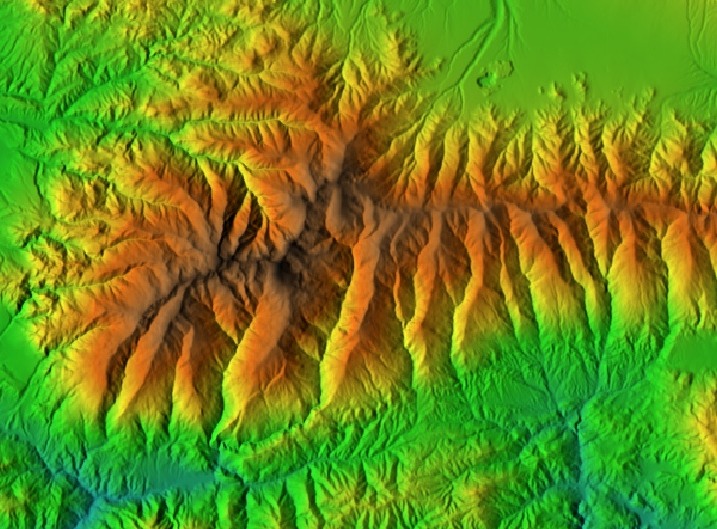DEM de Sierra Nevada.

 

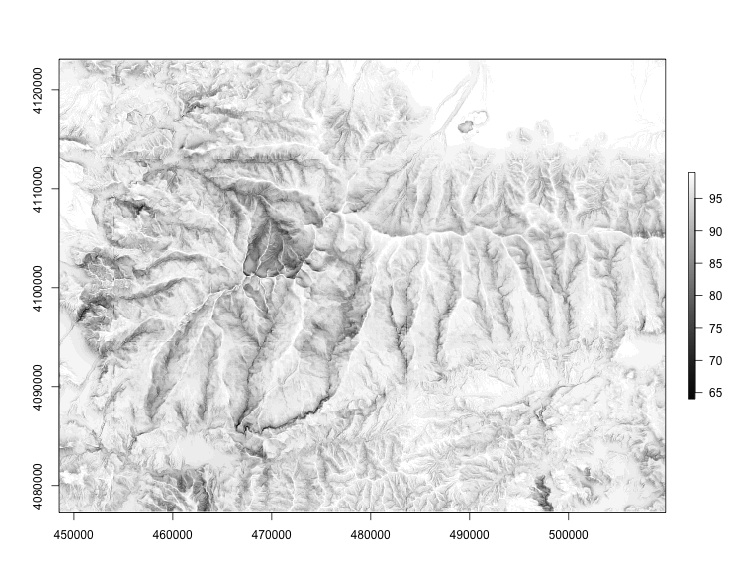
Cast shadows in Sierra Nevada with sun at 25° elevation, 215° azimut.

 

Illumination intensity on Sierra Nevada slopes with the sun in a hypothetical position of 45° elevation, 315° azimut.

 

Skyview factor in the Sierra Nevada.

 

Para los mapas promedio de insolación se utilizan datos climáticos a largo plazo, reanálisis climáticos como el NCEP CFS o ERA ECMWF, datos satelitales de la cubierta de nubes, mediciones de radiación cuando las hay disponibles, y parámetros adicionales para calcular la transmitancia atmosférica tales como turbidez de Linke o visibilidad. También comprobamos los mejores modelos para la irradiación difusa con los datos disponibles, y evaluamos el trabajo específico para el área de estudio (por ejemplo Boland et al 2008, 2013;. Dervishi et al 2012;. Jacovides et al 2006;. Liu y Jordan, 1960;. Pesadillo et al 2009; Ridley et al 2010;. Ruiz-Arias et al 2010; Torres et al 2010). Esto produce un mapa más realista de los valores que se pueden esperar en cada lugar en un día medio.

Usamos todo esto, junto con la posición solar, algoritmos astronómicos, la transmitancia atmosférica y los datos climáticos a largo plazo para crear un mapa de muy alta resolución de la superficie de la radiación solar. Puede comprobar cómo el proceso detecta el relieve a escala de rios y barrancos.

El proceso es largo e intensivo en CPU, pero no hay límite a la resolución que podemos ofrecer. Con las herramientas actuales de lidar o drones para crear mapas, podemos aumentar la resolución hasta los tejados de casas individuales. Póngase en contacto con nosotros si tiene algún requerimiento especifico en relación con los mapas de radiación solar.

 

References